Introduction
I completed this project in the Spring of 2024 along with four other Columbia University students: Julia Leviev, Nipun Agarwal, Brandon Zhang, and Yang Fengrui.
This project aims to harness advanced machine learning techniques to predict the malignancy of breast cancer cells from biopsy data. This is a critical problem, as diagnostic errors significantly affect cancer treatment outcomes. Research indicates that nearly 40% of these errors lead to severe consequences, including death. By leveraging machine learning models capable of analyzing complex biomedical data, we aim to develop a predictive model that reduces these errors by supplementing traditional diagnostic processes.
Data Preparation and Exploratory Analysis
The dataset consists of 569 samples of cancer cell characteristics extracted from digitalized images of breast mass tissue biopsies. Not counting an ID column, There are 30 numerical features in this dataset, primarily describing 10 visual characteristic (radius, texture, perimeter, area, smoothness, compactness, concavity, concave points, symmetry, and fractal_dimension), each with three measurements (standard error, average, and worst value). The target value (the diagnosis of the cell) is a binary variable encoded as “B” for benign and “M” for malignant. The various topological dimensions captured in this dataset allows for nuanced analysis of cell features to potentially differentiate between benign (357 samples) and malignant (212 samples) cases. The dataset is available here
When creating boxplots for each feature, our exploratory data analysis revealed that there were outliers in the data. However, we have no reason to believe that they are medically impossible or that the method of data collection has issues, so we accept them as part of our dataset population. Finally, to split our data, we allocated 20% of the dataset as test data using stratified split, and the rest served as our development set.
The dataset had no missing values, so there was no need for cleaning in that regard. The target variable was encoded as 0 (benign) and 1 (malignant), aligning with common practices for binary classification tasks. We did not observe significant sparsity either. Since initial exploratory analysis revealed that data was numerical, we used standard scaling on each of the features to mitigate issues with models that are not scale-invariant.
We also checked for correlated pairs of features above 0.9 using Pearson’s correlation coefficient. In particular, we noticed that the area, perimeter, and radius measurements were highly correlated. Since these three have a clear mathematical relationship, we felt we could safely choose one of the three as a representative variable. In addition to following best practices of eliminating redundant data, we did this to help with model interpretability, especially important given that our problem is in the biomedical space.
Linear models are especially prone to multicollinearity when it comes to interpretability, often oscillating between two correlated features when assigning feature importances. Even models that stably assign feature importances to one feature over the other correlated feature require special attention (e.g. even if the radius is consistently “chosen” over area as an important feature, it doesn’t mean that area isn’t important), so identifying correlated features and determining the retained feature’s meaning early on is a step that makes our models more interpretable. Therefore, we retained radius_se (radius_standard_error) and radius_mean over the rest. Other features retained include concavity_mean over concave_points_mean and concave_points_worst, as well as texture_mean over texture_worst.
Creating Classifiers
Logistic Regression
For our implementation of logistic regression, we used elastic-net since it can help perform feature selection but also imposes L2 regularization to help combat overfitting.
The elastic logistic regression model performs well. The model has a high ability to correctly identify both malignant tumors and benign tumors, as indicated by its 98.25% accuracy. Furthermore, it has a high recall score, clocking in at 95.24%.
The model has a high AUC score of 0.995 indicate the excellent model's ability to distinguish between malignant and benign tumors across all possible thresholds.
The Top ten features found are shown to the left. We have radius_se and radius_mean as the highest impact features. We can also see that the model made some of the features' coefficients to go to zero indicating that they dont have a lot of impact on the prediciton (in particular, the texture standard error and smoothness standard error).
Random Forest
Since this data contains many features, it isn't immediately obvious which are informative for prediction making. For that reason we are implementing a random forest. By taking random subsets of predictors, this model will cleverly determine feature importances and figure out the most effective way to divide the data to make predictions. Also, since the trees are uncorrelated, this model will ideally promote generalization and avoid overfitting on training data.
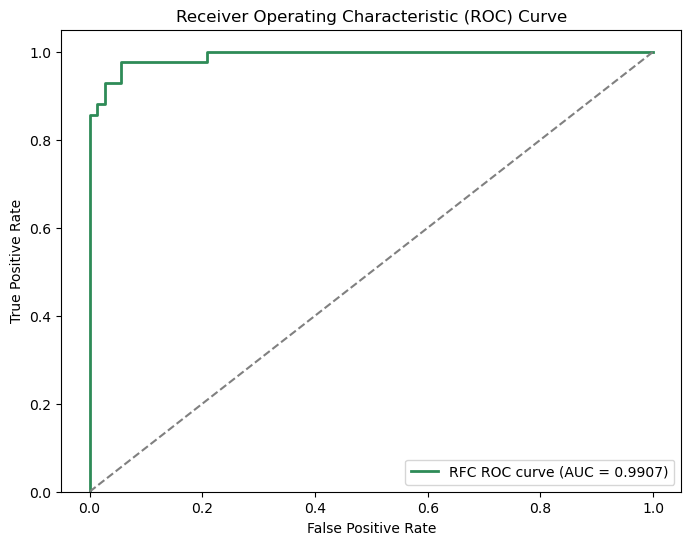
While the model maintains a 94% accuracy, it surprisingly falls short for recall, with a score of 88.10%. This indicates that when looking from the perspective of both classes the model is able to make decent predictions, but when focusing on the positive class (malignant) we see that it struggles.
Overall, the model's ability to distinguish positive samples from negative samples is quite good, with an AUC of 0.9907.
For a given feature, Random Forests determine importance by considering likelihood of reaching nodes corresponding to the feature as well as the information gain for each node. From the feature importances graph, we can see that Random Forest considers radius_mean and concavity_worst to be the top two features.
Boosted Models
Boosted models are another popular technique used for classification problems, where learners are sequentially trained based on the previous' mistakes to yield a final effective model. According to a study done by Cornell, empirically boosted models tended to perform best across measured metrics such as accuracy, f1-score, etc. While the study notes that even the "best" model can rank poorly on some datasets due to variability, the aggregate strong empirical results suggest that it is still worth implementing these models to see how they perform.
We tested three popular implementations of gradient-boosted models: XgBoost, HistGradientBoostingClassifier, and LightGBM. Our data is not sparse and does not have obvious monotonicity constraints, so all three techniques are applicable.
We used RandomSearch here, so there is always the caveat that a particular model may have gotten "lucky" with a hyperparameter search. But RandomSearch is generally shown to work well empirically, and makes our search over what would otherwise be a large state space much more tractable.
Out of the three boosted implementations, LightGBM performed the best in every metric (95.24% recall, 97.37% accuracy, 97.56% precision, and 0.9950 AUC), indicating that it not only performs well for our optimized metric (recall), but also performs well holistically. XGBoost performed the second best across all metrics, and HistGradientBoostedClassifier clearly struggled in comparison to the other two.
Looking at all three models, each consistently ranked radius_mean as a top-3 important feature. Concavity and symmetry related features also ranked highly all three models. Note that for HistGradientBoostedClassifier, the sklearn implementation does not come with feature importances, so we used permutation importances for this model.
XgBoost
HistGradientBoostingClassifier
LightGBM
K Nearest Neighbors
While k-Nearest Neighbors (kNN) classifier was initially selected for its simplicity, the use of grid search and stratified K-fold cross-validation helped optimize the model to achieve strong scores in precision and accuracy, with scores of 97.44% and 95.61% respectively. However, the 90.48% recall score indicates a slight struggle to classify true positives correctly compared to other models.
Permutation feature importance analysis highlighted key attributes that significantly affect the model's predictions. Features such as 'radius_mean' and 'smoothness_mean' are considered pivotal by the model, suggesting their strong relationship with the outcomes. On the other hand, features with negative importance scores, like 'symmetry_se', may not be as relevant and could be candidates for exclusion in simplifying the model, provided that domain expertise supports this decision.
Seen as a whole, the kNN model excelled in distinguishing cancer diagnoses, with 'manhattan' metric emerging as an effective distance calculation method. However, our focus on recall suggests that we should be wary given the slightly lower recall score relative to other models. The findings from feature importance offer a direction for further model refinement and could contribute to the development of more streamlined and interpretable diagnostic tools. However, it's important to approach feature selection with caution, ensuring that medical relevance is not compromised.
SVM
Based on hyperparameter tuning, the best model was determined to be a linear SVM with a high C value. This indicates a linear decision boundary and high penalty for errors was able to still achieve a reasonably high accuracy of around 94%. The recall and precision were over 92% as well. However, with a score of 0.9762 the AUC struggled in comparison with the other models, indicating that it has some issues ranking positive samples over negative samples.
Since the optimal model determined by hyperparameter tuning used a linear kernel, the feature importances are the weights the model assigned to each feature. From the feature importance chart, we can see that SVM considers smoothness_mean and concave points_se (standard error of the concave points) to be the two most impactful features.
Jupyter Notebook
Project Report
Conclusions
Overall, Logistic Regression clearly outperforms the rest of the models, with the highest accuracy, recall, precision, and AUC scores. So it excels both as a whole and for our optimized metric (recall).
However, all models were able to learn useful relationships from the data, as they nearly all achieved 90% in every reported metric. One benefit of training such a wide variety of proficient models is that we were able to observe feature importances for all of them, and extract the ones that occur consistently across all of them. In particular: concavity_mean, concavity_worst, radius_se (radius standard error), radius_mean, and smoothness_mean.
This information could be incredibly helpful for medical professionals, letting them know which attributes to focus on when making their diagnoses. Of course, domain knowledge should always be taken into account, so we hope that our insights can be used to supplement existing knowledge or at least provide future avenues for research.
Future directions include integrating these models with clinical diagnostic tools to provide real-time, data-driven insights to oncologists, thereby improving treatment decisions and patient outcomes.